关于科研相关的数理基础学习同搞科研本身的关系的基本讨论。讨论的是机器学习这个大方向,而不是物理,数学,生物这些方向。
问题描述
同科研相关的数理基础的学习能极大的提高搞出好科研的可能性和上限,甚至能加快平时搞科研的效率。这是讨论的前提:数理知识(概率论和一些分析,主要是概率论对分析有要求)对搞科研有帮助,尤其是机器学习顶会方向。但是搞科研本身又是一件很消耗时间的事情,同打数理基础的时间消耗直接构成了竞争关系。所以需要讨论一下两者间基本的关系:对于数理基础不足的同学(比如我,数学和代码都弱),在打牢数理基础之前的这段时间内(这是一个很长期的过程,王老师都当上正教授了,至今还在每天看各类数学书籍),如何处理好科研本身同基础技能之间的时间分配。思路主要是分析边际增益和边际成本那一套。下面一点点的建模。(搞个微分方程也能搞搞)
基础技能学习的总收益与边际增益
基础技能学习的特点就是没事多看书,做练习总会有提升,相对可控一点。基础技能学习层次由低到高、由实在到抽象的过程是:基本概念的定义(看过定义总会有印象,所谓“用到了再学”大多就这个层次,聪明一点的高中生就能办到),计算方法的梳理(就是哪个问题怎么算,具体计算过程,一般大学临时抱佛脚就这个层次),基本判断能力的建立(别人的逻辑中出了漏洞你能揪出来,学分析中会有一点锻炼),能自己产生解决问题的思路(冯睿蠡差不多有这个能力,啥事都能讲出个叫人信服的123),你能解决实际问题了(下面我也不知道怎么编了,我又没到过这个境界,自然不知道)。(看定义—>看总结—>看证明—>做题—>做难题)。
所以我就需要考察学习一段时间同这几个能力之间是啥关系喽。比如设基础技能的学习总收益是上面5个量的加权和,能力越抽象,效益越大,但是越难增长。
其中$a_1=0.1;a_{2}=0.1;a_{3}=0.1;a_{4}=0.3;a_{5}=0.4$,表示了它们对做科研的重要程度;
同时$\alpha_1=0.1;\alpha_{2}=0.1;\alpha_{3}=0.2;\alpha_{4}=0.3;\alpha_{5}=0.3$,表示了实际在看书时的时间分配;
而这5个层面关于投入时间的关系又有着不同的特点:$g_{c}(t)$以较大的斜率线性增长;$g_{m}(t)$以中等的斜率线性增长;$g_{j}(t)$以对数曲线速度增长;$g_{t}(t)$以中等的斜率,沿着线性函数阶梯式增长,禁区中等(以小时记);$g_{s}(t)$以沿着对数函数阶梯式增长,禁区长(以天记);观察下面粗略估计的曲线,持续一个月以上才能对某个章节有个相对对科研有帮助的理解程度(3周6天2小时)。
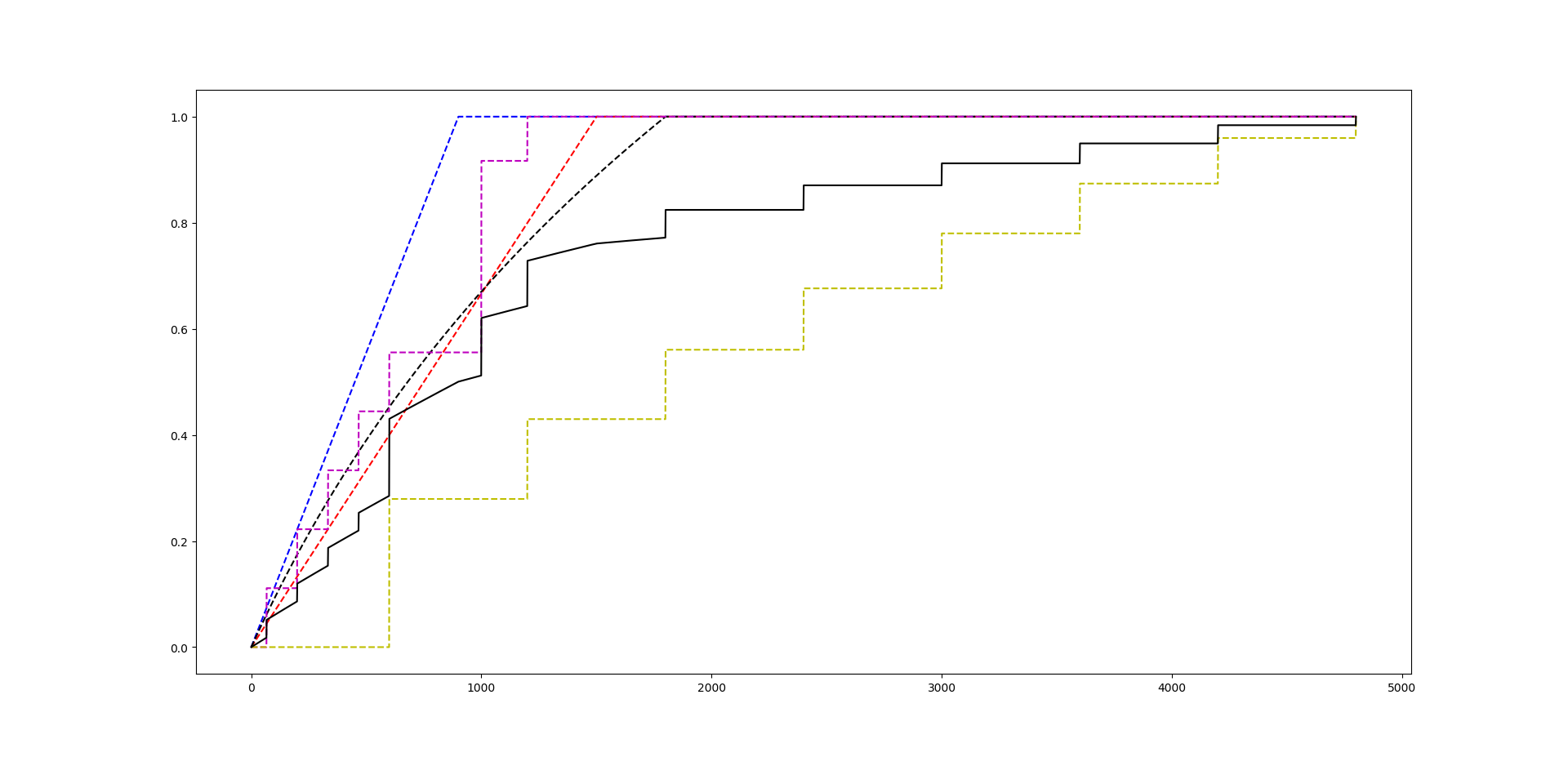
蓝线表示对概念的熟知,红线表示对计算过程的了解,黑虚线表示对证明过程的掌握,紫线表示对概念及方法应用的题目的掌握,黄线表示对难题,需要深入思考的题目的掌握程度。横轴表示分钟,纵轴表示掌握程度,最高为1。黑实线为总的收益。